O conjunto dos números racionais (representado por
 ) é definido por:
) é definido por:São exemplos de números racionais:

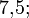
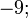

![\sqrt[2]{4};](http://upload.wikimedia.org/math/0/3/a/03acd2e46032e91523c3ee6d458c6ba5.png)

Os números racionais opõem-se aos números irracionais (
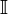 ).
).Para representar o conjunto dos racionais não negativos podemos usar
 e para representar o conjunto dos números racionais não positivos podemos utilizar
e para representar o conjunto dos números racionais não positivos podemos utilizar  O número zero também faz parte do conjunto dos racionais. É comum usar um asterisco ao lado do símbolo que representa um determinado conjunto para indicar que se retirou o zero do mesmo, como em
O número zero também faz parte do conjunto dos racionais. É comum usar um asterisco ao lado do símbolo que representa um determinado conjunto para indicar que se retirou o zero do mesmo, como em  (números racionais não nulos),
(números racionais não nulos),  (racionais positivos) e
(racionais positivos) e 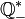 (racionais negativos). [carece de fontes]
(racionais negativos). [carece de fontes]Há quatro formas de se apresentarem os números racionais: Frações (próprias ou impróprias), números mistos (que é uma variação das frações impróprias), números decimais de escrita finita e, por fim, as dízimas, que são números decimais em cuja escrita aparecem períodos numéricos infinitos. Eis alguns exemplos:
- Fração:

- Numeral misto: 5

- Números decimais de escrita finita: 8,35;
- Dízimas periódicas: 8,(23); 1,23(5); 7,23(965);
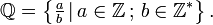

Nenhum comentário:
Postar um comentário