NÚMEROS INTEIROS RELATIVOSINTRODUÇÃO:
Observe que, no conjunto dos números naturais, a operação de subtração nem sempre é possivel
exemplos:
a) 5 - 3 = 2 (possível: 2 é um número natural)
b) 9 - 9 = 0 ( possível: 0 é um número natural)
c) 3 - 5 = ? ( impossível nos números naturais)
Para tonar sempre possível a subtração, foi criado o conjunto dos números inteiros relativos,
-1, -2, -3,.........
lê-se: menos um ou 1 negativo
lê-se: menos dois ou dois negativo
lê-se: menos três ou três negativo
Reunindo os números negativos, o zero e os números positivos, formamos o conjunto dos numeros inteiros relativos, que será representado por Z.
Z = { .....-3, -2, -1, 0, +1, +2, +3,......}
Importante: os números inteiros positivos podem ser indicados sem o sinal de +.
exemplo
a) +7 = 7
b) +2 = 2
c) +13 = 13
d) +45 = 45
Sendo que o zero não é positivo nem negativo
EXERCICIOS
1) Observe os números e diga:
-15, +6, -1, 0, +54, +12, -93, -8, +23, -72, +72
a) Quais os números inteiros negativos?
R: -15,-1,-93,-8,-72
b) Quais são os números inteiros positivos?
R: +6,+54,+12,+23,+72
2) Qual o número inteiro que não é nem positivo nem negativo?
R: É o zero
3) Escreva a leitura dos seguintes números inteiros:
a) -8 =
(R: oito negativo)
b)+6 =
(R: seis positivo)
c) -10 =
(R: dez negativo)
d) +12 =
(R: doze positivo)
e) +75 =
(R: setenta e cinco positivo)
f) -100 =
(R: cem negativo)
4) Quais das seguintes sentenças são verdadeiras?
a) +4 = 4 =
( V)
b) -6 = 6 =
( F)
c) -8 = 8 =
( F)
d) 54 = +54 =
( V)
e) 93 = -93 =
( F )
5) As temperaturas acima de 0°C (zero grau) são representadas por números positivos e as temperaturas abaixo de 0°C, por números negativos. Represente a seguinte situação com números inteiros relativos:
a) 5° acima de zero =
(R: +5)
b) 3° abaixo de zero =
(R: -3)
c) 9°C abaixo de zero=
(R: -9)
d) 15° acima de zero =
( +15)
REPRESENTAÇÃO DOS NÚMEROS INTEIROS NA RETA
Vamos traçar uma reta e marcar o ponto 0. À direta do ponto 0, com uma certa unidade de medida, assinalemos os pontos que correspondem aos números positivos e à esquerda de 0, com a mesma unidade, assinalaremos os pontos que correspondem aos números negativos.
_I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
exercícios
1) Escreva os números inteiros:
a) compreendidos entre 1 e 7
(R: 2,3,4,5,6)
b) compreendidos entre -3 e 3
(R: -2,-1,0,1,2)
c) compreendidos entre -4 e 2
( R: -3, -2, -1, 0, 1)
d) compreendidos entre -2 e 4
(R: -1, 0, 1, 2, 3 )
e) compreendidos entre -5 e -1
( R: -4, -3, -2)
f) compreendidos entre -6 e 0
(R: -5, -4, -3, -2, -1)
2) Responda:
a) Qual é o sucessor de +8?
(R: +9)
b) Qual é o sucessor de -6?
(R: -5)
c) Qual é o sucessor de 0 ?
(R: +1)
d) Qual é o antecessor de +8?
(R: +7)
e) Qual é o antecessor de -6?
( R: -7)
f) Qual é o antecessor de 0 ?
( R: -1)
3) Escreva em Z o antecessor e o sucessor dos números:
a) +4
(R: +3 e +5)
b) -4
(R: -5 e - 3)
c) 54
(R: 53 e 55 )
d) -68
(R: -69 e -67)
e) -799
( R: -800 e -798)
f) +1000
(R: +999 e + 1001)
NÚMEROS OPOSTOS E SIMÉTRICOS
Na reta numerada, os números opostos estão a uma mesma distancia do zero.
-I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
Observe que cada número inteiro, positivo ou negativo, tem um correspondente com sinais deferentes
exemplo
a) O oposto de +1 é -1.
b) O oposto de -3 é +3.
c) O oposto de +9 é -9.
d) O oposto de -5 é +5.
Obsevação: O oposto de zero é o próprio zero.
EXERCÍCIOS
1) Determine:
a) O oposto de +5 =
(R:-5)
b) O oposto de -9 =
(R: +9)
c) O oposto de +6 =
(R: -6)
d) O oposto de -6 =
(R: +6)
e) O oposto de +18 =
(R: -18)
f) O oposto de -15 =
(R: +15)
g) O oposto de +234=
(R: -234)
h) O oposto de -1000 =
(R: +1000)
COMPARAÇÃO DE NÚMEROS INTEIROS ,
Observe a representação gráfica dos números inteiros na reta.
-I___I___I___I___I___I___I___I___I___I___I___I___I___I_
-6.. -5...-4. -3,. -2,..-1,.. 0,.+1,.+2,.+3,.+4,..+5,.+6
Dados dois números quaisquer, o que está à direita é o mair deles, e o que está à esquerda, o menor deles.
exemplos
a) -1 maior; -4, poque -1 está à direita de -4.
b) +2 maior; -4, poque +2 está a direita de -4
c) -4 menor -2 , poque -4 está à esquerda de -2.
d) -2 menor +1, poque -2 está à esquerda de +1.
exercicios
1) Qual é o número maior ?
a) +1 ou -10
(R:+1)
b) +30 ou 0
(R: +30)
c) -20 ou 0
( R: 0)
d) +10 ou -10
(R: +10)
e) -20 ou -10
(R: -10)
f) +20 ou -30
(R: +20)
g) -50 ou +50
(R:+50)
h) -30 ou -15
(R:-15)
2) compare os seguites pares de números, dizendo se o primeiro é maior, menor ou igual
a) +2 e + 3
(menor)
b) +5 e -5
(maior)
c) -3 e +4
(nenor)
d) +1 e -1
(maior)
e) -3 e -6
( maior)
f) -3 e -2
(menor)
g) -8 e -2
(menor)
h) 0 e -5
(maior)
i) -2 e 0
(nenor)
j) -2 e -4
(maior)
l) -4 e -3
(menor)
m) 5 e -5
(maior)
n) 40 e +40
( igual)
o) -30 e -10
(menor)
p) -85 e 85
(menor)
q) 100 e -200
(maior)
r) -450 e 300
(menor)
s) -500 e 400
(menor)
3) coloque os números em ordem crescente.
a) -9,-3,-7,+1,0
(R: -9,-7,-3,0,1)
b) -2, -6, -5, -3, -8
(R: -8, -6,-5, -3,-2)
c) 5,-3,1,0,-1,20
(R: -3,-1,0,1,5,20)
d) 25,-3,-18,+15,+8,-9
(R: -18,-9,-3,+8,+15,+25)
e) +60,-21,-34,-105,-90
( R: -105,-90,-34,-21, +60)
f) -400,+620,-840,+1000,-100
( R: -840,-400,-100,+620,+1000)
4) Coloque os números em ordem decrescente
a) +3,-1,-6,+5,0
(R: +5,+3,0,-1,-6)
b) -4,0,+4,+6,-2
( R: +6,+4,0,-2,-4)
c) -5,1,-3,4,8
( R: 8,4,1,-3,-5)
d) +10,+6,-3,-4,-9,+1
(R: +10,+6,+1,-3,-4,-9)
e) -18,+83,0,-172, -64
(R: +83,0,-18,-64,-172)
f) -286,-740, +827,0,+904
(R: +904,+827,0,-286,-740)
ADIÇÃO E SUBTRAÇÃO COM NÚMEROS INTEIROSADIÇÃO
1) Adição de números positivos
A soma de dois números positivos é um número positivo.
EXEMPLO
a) (+2) + (+5) = +7
b) (+1) + (+4) = +5
c) (+6) + (+3) = +9
Simplificando a maneira de escrever
a) +2 +5 = +7
b) +1 + 4 = +5
c) +6 + 3 = +9
Observe que escrevemos a soma dos números inteiros sem colocar o sinal + da adição e eliminamos os parêteses das parcelas.
2) Adição de números negativos
A soma de dois numeros negativos é um número negativo
Exemplo
a) (-2) + (-3) = -5
b) (-1) + (-1) = -2
c) (-7) + (-2) = -9
Simplificando a maneira de escrever
a) -2 - 3 = -5
b) -1 -1 = -2
c) -7 - 2 = -9
Observe que podemos simplificar a maneira de escrever deixando de colocar o sinal de + na operação e eliminando os parênteses das parcelas.
EXERCÍCIOS
1) Calcule
a) +5 + 3 =
(R:+8)
b) +1 + 4 =
(R: +5)
c) -4 - 2 =
(R: -6)
d) -3 - 1 =
(R: -4)
e) +6 + 9 =
(R: +15)
f) +10 + 7 =
(R: +17)
g) -8 -12 =
(R: -20)
h) -4 -15 =
(R: -19)
i) -10 - 15 =
(R: -25)
j) +5 +18 =
(R: +23)
l) -31 - 18 =
(R: -49)
m) +20 +40 =
(R: + 60)
n) -60 - 30 =
(R: -90)
o) +75 +15 =
(R: +90)
p) -50 -50 =
(R: -100)
2) Calcule:
a) (+3) + (+2) =
(R: +5)
b) (+5) + (+1) =
(R: +6)
c) (+7) + ( +5) =
(R: +12)
d) (+2) + (+8) =
(R: +10)
e) (+9) + (+4) =
(R: +13)
f) (+6) + (+5) =
(R: +11)
g) (-3) + (-2) =
(R: -5)
h) (-5) + (-1) =
(R: -6)
i) (-7) + (-5) =
(R: -12)
j) (-4) + (-7) =
(R: -11)
l) (-8) + ( -6) =
(R: -14)
m) (-5) + ( -6) =
(R: -11)
3) Calcule:
a) ( -22) + ( -19) =
(R: -41)
b) (+32) + ( +14) =
(R: +46)
c) (-25) + (-25) =
(R: -50)
d) (-94) + (-18) =
(R: -112)
e) (+105) + (+105) =
(R: +210)
f) (-280) + (-509) =
(R: -789)
g) (-321) + (-30) =
(R: -350)
h) (+200) + (+137) =
(R: +337)
3) Adição de números com sinais diferentes
A soma de dois números inteiros de sinais diferentes é obtida subtraindo-se os valores absolutos, dando-se o sinal do número que tiver maior valor absoluto.
exemplos
a) (+6) + ( -1) = +5
b) (+2) + (-5) = -3
c) (-10) + ( +3) = -7
simplificando a maneira de escrever
a) +6 - 1 = +5
b) +2 - 5 = -3
c) -10 + 3 = -7
Note que o resultado da adição tem o mesmo sinal que o número de maior valor absoluto
Observação:
Quando as parcelas são números opostos, a soma é igual a zero.
Exemplo
a) (+3) + (-3) = 0
b) (-8) + (+8) = 0
c) (+1) + (-1) = 0
simplificando a maneira de escrever
a) +3 - 3 = 0
b) -8 + 8 = 0
c) +1 - 1 = 0
4) Um dos numeros dados é zero
Quando um dos números é zero , a soma é igual ao outro número.
exemplo
a) (+5) +0 = +5
b) 0 + (-3) = -3
c) (-7) + 0 = -7
Simplificando a maneira de escrever
a) +5 + 0 = +5
b) 0 - 3 = -3
c) -7 + 0 = -7
exercícios
1) Calcule:
a) +1 - 6 =
-5
b) -9 + 4 =
-5
c) -3 + 6 =
+3
d) -8 + 3 =
-5
e) -9 + 11 =
+2
f) +15 - 6 =
+9
g) -2 + 14 =
+12
h) +13 -1 =
+12
i) +23 -17 =
+6
j) -14 + 21 =
+7
l) +28 -11 =
+17
m) -31 + 30 =
-1
2) Calcule:
a) (+9) + (-5) =
+4
b) (+3) + (-4) =
-1
c) (-8) + (+6) =
-2
d) (+5) + (-9) =
-4
e) (-6) + (+2) =
-4
f) (+9) + (-1) =
+8
g) (+8) + (-3) =
+5
h) (+12) + (-3) =
+9
i) (-7) + (+15) =
+8
j) (-18) + (+8) =
-10
i) (+7) + (-7) =
0
l) (-6) + 0 =
-6
m) +3 + (-5) =
-2
n) (+2) + (-2) =
0
o) (-4) +10 =
+6
p) -7 + (+9) =
+2
q) +4 + (-12) =
-8
r) +6 + (-4) =
+2
3) Calcule
a) (+5 + (+7) = +12
b) (-8) + (-9) = -17
c) (-37) + (+35) = -2
d) (+10) + (-9) = +1
e) (-15 ) + (+15) = 0
f) (+80) + 0 = +80
g) (-127) + (-51) = -178
h) (+37) + (+37) = +74
i) (-42) + (-18) = -60
j) (-18) + (+17) = -1
l) (-18) + (+19) = +1
m) (-1) + (-42) = -43
n) (+325) + (-257) = +68
o) 0 + (-75) = -75
p) (-121) + (+92) = -29
q ) (-578) + (-742) = -1320
r) (+101) + (-101) = 0
s) (-1050) + (+876) = -174
PROPRIEDADE DA ADIÇÃO
1)
Fechamento : a soma de dois números inteiros é sempre um número inteiro
exemplo (-4) + (+7) =( +3)
2)
Comutativa: a ordem das parcelas não altera a soma.
exemplo: (+5) + (-3) = (-3) + (+5)
3)
Elemento neutro: o número zero é o elemento neutro da adição.
exemplo: (+8) + 0 = 0 + (+8) = +8
4)
Associativa: na adição de três números inteiros, podemos associar os dois primeiros ou os dois últimos, sem que isso altere o resultado.
exemplo: [(+8) + (-3) ] + (+4) = (+8) + [(-3) + (+4)]
5)
Elemento oposto: qualquer número inteiro admite um simétrico ou oposto.
exemplo: (+7) + (-7) = 0
ADIÇÃO DE TRÊS OU MAIS NÚMEROS
Para obter a soma de três ou mais números adicionamos os dois primeiros e, em seguida, adicionamos esse resultado com o terceiro, e assim por diante.
exemplos
1) -12 + 8 - 9 + 2 - 6 =
= -4 - 9 + 2 - 6 =
= -13 + 2 - 6 =
= -11 - 6 =
= -17
2) +15 -5 -3 +1 - 2 =
= +10 -3 + 1 - 2 =
= +7 +1 -2 =
= +8 -2 =
= +6
Na adição de números inteiros podemos cancelar números opostos, poque a soma deles é zero.
INDICAÇÃO SIMPLIFICADA
a) podemos dispensar o sinal de + da primeira parcela quando esta for positiva.
exemplos
a) (+7) + (-5) = 7 - 5 = +2
b) (+6) + (-9) = 6 - 9 = -3
b) Podemos dispensar o sinal + da soma quando esta for positiva
exemplos
a) (-5) + (+7) = -5 + 7 = 2
b) (+9) + (-4) = 9 - 4 = 5
EXERCÍCIOS
1) Calcule
a) 4 + 10 + 8 = (R: 22)
b) 5 - 9 + 1 = (R: -3)
c) -8 - 2 + 3 = (R: -7)
d) -15 + 8 - 7 = (R: -14)
e) 24 + 6 - 12 = (R:+18)
f) -14 - 3 - 6 - 1 = (R: -24)
g) -4 + 5 + 6 + 3 - 9 = (R: + 1)
h) -1 + 2 - 4 - 6 - 3 - 8 = (R: -20)
i) 6 - 8 - 3 - 7 - 5 - 1 + 0 - 2 = (R: -20)
j) 2 - 10 - 6 + 14 - 1 + 20 = (R: +19)
l) -13 - 1 - 2 - 8 + 4 - 6 - 10 = (R: -36)
2) Efetue, cancelando os números opostos:
a) 6 + 4 - 6 + 9 - 9 = (R: +4)
b) -7 + 5 - 8 + 7 - 5 = (R: -8)
c) -3 + 5 + 3 - 2 + 2 + 1 = (R: +6)
d) -6 + 10 + 1 - 4 + 6= (R: +7)
e) 10 - 6 + 3 - 3 - 10 - 1 = (R: -7)
f) 15 - 8 + 4 - 4 + 8 - 15 = (R: 0)
3) Coloque em forma simplificada ( sem parênteses)
a) (+1) + (+4) +(+2) = (R: 1 +4 + 2)
b) (+1) + (+8) + (-2) = (R: 1 + 8 - 2)
c) (+5) +(-8) + (-1) = (R: +5 - 8 - 1)
d) (-6) + (-2) + (+1) = (R: -6 - 2 + 1)
4) Calcule:
a) (-2) + (-3) + (+2) = (R: -3)
b) (+3) + (-3) + (-5) = (R: -5)
c) (+1) + (+8) +(-2) = (R: +7 )
d) (+5) + (-8) + (-1) = (R: -4)
e) (-6) + (-2) + (+1) = (R: -7)
f) (-8) + ( +6) + (-2) = (R: -4)
g) (-7) + 6 + (-7) = (R: -8)
h) 6 + (-6) + (-7) = (R: -7)
i) -6 + (+9) + (-4) = (R: -1)
j) (-4) +2 +4 + (+1) = (R: +3)
5) Determine as seguintes somas
a) (-8) + (+10) + (+7) + (-2) = (R: +7)
b) (+20) + (-19) + (-13) + (-8) = (R: -20)
c) (-5) + (+8) + (+2) + (+9) = (R: +14)
d) (-1) + (+6) + (-3) + (-4) + (-5) = (R: -7)
e) (+10) + (-20) + (-15) + (+12) + (+30) + (-40) = (R: -23)
f) (+3) + (-6) + (+8) =
(R: +5)
g) (-5) + (-12) + (+3) = (R: -14)
h) (-70) + (+20) + (+50) =
(R: 0)
i) (+12) + (-25) + (+15) = (R: +2)
j) (-32) + (-13) + (+21) = (R: -24)
l) (+7) + (-5) + (-3) + (+10) = (R: +9)
m) (+12) + (-50) + (-8) + (+13) =
(R: -33)
n) (-8)+(+4)+ (+8) + (-5) + (+3) = (R: +2)
o) (-36) + (-51) + (+100) + (-52) =
(R: -39)
p) (+17) + (+13) + (+20) + (-5) + (-45) =
(R:0)
6) Dados os números x= 6, y = 5 e z= -6, calcule
a) x + y = (R: +11)
b) y + z = (R: -4)
c) x + z = (R: -3)
SUBTRAÇÃO
A operação de subtração é uma operação inversa à da adição
Exemplos
a) (+8) - (+4) = (+8) + (-4) = = +4
b) (-6) - (+9) = (-6) + (-9) = -15
c) (+5) - (-2) = ( +5) + (+2) = +7
Conclusão: Para subtraimos dois números relativos, basta que adicionemos ao primeiro o oposto do segundo.
Observação: A subtração no conjunto Z tem apenas a propriedade do fechamento ( a subtração é sempre possivel)
ELIMINAÇÃO DE PARÊNTESES PRECEDIDOS DE SINAL NEGATIVO
Para facilitar o cálculo, eliminamos os parênteses usando o segnificado do oposto
veja:
a) -(+8) = -8 (significa o oposto de +8 é -8 )
b) -(-3) = +3 (significa o oposto de -3 é +3)
analogicamente:
a) -(+8) - (-3) = -8 +3 = -5
b) -(+2) - (+4) = -2 - 4 = -6
c) (+10) - (-3) - +3) = 10 + 3 - 3 = 10
conclusão: podemos eliminar parênteses precedidos de sinal negativo trocando-se o sínal do número que está dentro dos parênteses.
EXERCÍCIOS
1) Elimine os parênteses
a) -(+5) =
-5
b) -(-2) =
+2
c) - (+4) =
-4
d) -(-7) =
+7
e) -(+12) =
-12
f) -(-15) =
+15
g) -(-42) =
+42
h) -(+56) =
-56
2) Calcule:
a) (+7) - (+3) =
(R: +4)
b) (+5) - (-2) =
(R: +7)
c) (-3) - ( +8) =
(R: -11)
d) (-1) -(-4) =
(R: +3)
e) (+3) - (+8) =
(R: -5)
f) (+9) - (+9) =
(R: 0 )
g) (-8) - ( +5) =
(R: -13)
h) (+5) - (-6) =
(R: +11)
i) (-2) - (-4) =
(R: +2)
j) (-7) - (-8) =
(R: +1)
l) (+4) -(+4) =
(R: 0)
m) (-3) - ( +2) =
(R: -5)
n) -7 + 6 =
(R: -1)
o) -8 -7 =
(R: -15)
p) 10 -2 =
(R: 8)
q) 7 -13 =
(R: -6)
r) -1 -0 =
(R: -1)
s) 16 - 20 =
(R: -4)
t) -18 -9 =
(R: -27)
u) 5 - 45 =
(R:-40)
v) -15 -7 =
(R: -22)
x) -8 +12 =
(R: 4)
z) -32 -18 =
(R:-50)
3) Calcule:
a) 7 - (-2) =
(R: 9)
b) 7 - (+2) =
(R: 5)
c) 2 - (-9) =
(R: 11)
d) -5 - (-1) =
(R: -4)
e) -5 -(+1) =
(R: -6)
f) -4 - (+3) =
(R: -7)
g) 8 - (-5) =
(R: 13)
h) 7 - (+4) =
(R: 3)
i) 26 - 45 =
(R: -19)
j) -72 -72 =
(R: -144)
l) -84 + 84 =
(R: 0)
m) -10 -100 =
(R: -110)
n) -2 -4 -1 =
(R: -7)
o) -8 +6 -1 =
(R: -3)
p) 12-7 + 3 =
(R: 8)
q) 4 + 13 - 21 =
(R: -4)
r) -8 +8 + 1 =
(R: 1)
s) -7 + 6 + 9 =
(R: 8)
t) -5 -3 -4 - 1 =
(R: -13)
u) +10 - 43 -17 =
(R: -50)
v) -6 -6 + 73 =
(R: 61)
x) -30 +30 - 40 =
(R: -40)
z) -60 - 18 +50 =
(R: -28)
4) Calcule:
a) (-4) -(-2)+(-6) =
(R: -8)
b) (-7)-(-5)+(-8) =
(R: -10)
c) (+7)-(-6)-(-8) =
(R: 21)
d) (-8) + (-6) -(+3) =
(R: -17)
e) (-4) + (-3) - (+6) =
(R: -13)
f) 20 - (-6) - (-8) =
(R: 34)
g) 5 - 6 - (+7) + 1 =
(R: -7)
h) -10 - (-3) - (-4) =
(R: -3)
i) (+5) + (-8) =
(R: -3)
j) (-2) - (-3) =
(R: +1)
l) (-3) -(-9) =
(R: +6)
m) (-7) - (-8) =
(R: +1)
n) (-8) + (-6) - (-7) =
(R: -7)
o) (-4) + (-6) + (-3) =
(R: -13)
p) 15 -(-3) - (-1) =
(R: +19)
q) 32 - (+1) -(-5) =
(R: +36)
r) (+8) - (+2) =
(R:+6)
s) (+15) - (-3) =
(R: +18)
t) (-18) - (-10) =
(R: -8)
u) (-25) - (+22) =
(R:-47)
v) (-30) - 0 =
(R: -30)
x) (+180) - (+182) =
(R: -2)
z) (+42) - (-42) =
(R: +84)
5) Calcule:
a) (-5) + (+2) - (-1) + (-7) =
(R: -9)
b) (+2) - (-3) + (-5) -(-9) =
(R: 9)
c) (-2) + (-1) -(-7) + (-4) =
(R: 0)
d) (-5) + (-6) -(-2) + (-3) =
(R: -12)
e) (+9) -(-2) + (-1) - (-3) =
(R: 13)
f) 9 - (-7) -11 =
(R: 5 )
g) -2 + (-1) -6 =
(R: -9)
h) -(+7) -4 -12 =
(R: -23)
i) 15 -(+9) -(-2) =
(R: 8 )
j) -25 - ( -5) -30 =
(R: -50)
l) -50 - (+7) -43 =
(R: -100)
m) 10 -2 -5 -(+2) - (-3) =
(R: 4)
n) 18 - (-3) - 13 -1 -(-4) =
(R: 11)
o) 5 -(-5) + 3 - (-3) + 0 - 6 =
(R: 10)
p) -28 + 7 + (-12) + (-1) -4 -2 =
(R: -40)
q) -21 -7 -6 -(-15) -2 -(-10) =
(R: -11)
r) 10 -(-8) + (-9) -(-12)-6 + 5 =
(R: 20)
s) (-75) - (-25) =
(R: -50)
t) (-75) - (+25) =
(R: -100)
u) (+18) - 0 =
(R: +18)
v) (-52) - (-52) =
(R:0)
x) (-16)-(-25) =
(R:+9)
z) (-100) - (-200) =
(R:+100)
ELIMINAÇÃO DOS PARENTESES
1) parenteses precedidos pelo sinal +
Ao eliminarmos os parênteses e o sinal + que os precede, devemos conservar os sinais dos números contidos nesses parênteses.
exemplo
a) + (-4 + 5) = -4 + 5
b) +(3 +2 -7) = 3 +2 -7
2) Parênteses precedidos pelo sinal -
Ao eliminarmos os parênteses e o sinal de - que os precede, devemos trocar os sinais dos números contidos nesses parênteses.
exemplo
a) -(4 - 5 + 3) = -4 + 5 -3
b) -(-6 + 8 - 1) = +6 -8 +1
EXERCICIOS
1) Elimine os parênteses:
a) +(-3 +8) =
(R: -3 + 8)
b) -(-3 + 8) =
(R: +3 - 8)
c) +(5 - 6) =
(R: 5 -6 )
d) -(-3-1) =
(R: +3 +1)
e) -(-6 + 4 - 1) =
(R: +6 - 4 + 1)
f) +(-3 -2 -1) =
(R: -3 -2 -1 )
g) -(4 -6 +8) =
(R: -4 +6 +8)
h) + (2 + 5 - 1) =
(R: +2 +5 -1)
2) Elimine os parênteses e calcule:
a) + 5 + ( 7 - 3) =
(R: 9)
b) 8 - (-2-1) =
(R: 11)
c) -6 - (-3 +2) =
(R: -5)
d) 18 - ( -5 -2 -3 ) =
(R: 28)
e) 30 - (6 - 1 +7) =
(R: 18)
f) 4 + (-5 + 0 + 8 -4) =
(R: 3)
g) 4 + (3 - 5) + ( -2 -6) =
(R: -6)
h) 8 -(3 + 5 -20) + ( 3 -10) =
(R: 13)
i) 20 - (-6 +8) - (-1 + 3) =
(R: 16)
j) 35 -(4-1) - (-2 + 7) =
(R: 27)
3) Calcule:
a) 10 - ( 15 + 25) =
(R: -30)
b) 1 - (25 -18) =
(R: -6)
c) 40 -18 - ( 10 +12) =
(R: 0)
d) (2 - 7) - (8 -13) =
(R: 0 )
e) 7 - ( 3 + 2 + 1) - 6 =
(R: -5)
f) -15 - ( 3 + 25) + 4 =
(R: -39)
g) -32 -1 - ( -12 + 14) =
(R: -35)
h) 7 + (-5-6) - (-9 + 3) =
(R: 2)
i) -(+4-6) + (2 - 3) =
(R: 1)
j) -6 - (2 -7 + 1 - 5) + 1 =
(R: 4)
 ) é definido por:
) é definido por:
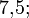
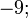

![\sqrt[2]{4};](http://upload.wikimedia.org/math/0/3/a/03acd2e46032e91523c3ee6d458c6ba5.png)

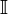 ).
). e para representar o conjunto dos números racionais não positivos podemos utilizar
e para representar o conjunto dos números racionais não positivos podemos utilizar  O número zero também faz parte do conjunto dos racionais. É comum usar um asterisco ao lado do símbolo que representa um determinado conjunto para indicar que se retirou o zero do mesmo, como em
O número zero também faz parte do conjunto dos racionais. É comum usar um asterisco ao lado do símbolo que representa um determinado conjunto para indicar que se retirou o zero do mesmo, como em  (números racionais não nulos),
(números racionais não nulos),  (racionais positivos) e
(racionais positivos) e 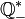 (racionais negativos). [carece de fontes]
(racionais negativos). [carece de fontes]

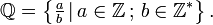


 para se referir ao conjunto de todos os números naturais. Este conjunto é infinito e
para se referir ao conjunto de todos os números naturais. Este conjunto é infinito e 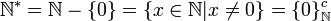
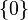 , pois 0 é o
, pois 0 é o  , que indicava o agrupamento.
, que indicava o agrupamento.





