0,05 = 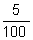 = 5% = 5% |
1,17 = 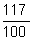 = 117% = 117% |
5,8 = 5,80 = 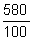 = 580% = 580%
Operações com números
racionais decimais
Divisão
1º: Divisão exata
Considere a seguinte divisão: 1,4 :
0,05
Transformando em frações decimais, temos:
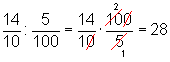
Método prático
1º) Igualamos o números de casas
decimais, com o acréscimo de zeros;
2º) Suprimimos as vírgulas;
3º)
Efetuamos a divisão. |
Exemplos:
| Igualamos as casa
decimais: |
1,40 |
: |
0,05 |
| Suprimindo as
vírgulas: |
140 |
: |
5 |
Logo, o quociente de 1,4 por 0,05 é
28.
|
Efetuado a divisão
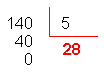 |
| Igualamos as casas
decimais |
6,000 |
: |
0,015 |
| Suprimindo as
vírgulas |
6.000 |
: |
15 |
Logo, o quociente de 6 por 0,015 é
400.
|
Efetuando a divisão
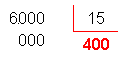 |
| Igualamos as casas
decimais |
4,096 |
: |
1,600 |
| Suprimindo as
vírgulas |
4.096 |
: |
1.600 |
|
Efetuando a divisão
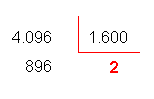 |
Observe que na divisão acima o quociente inteiro é 2
e o resto corresponde a 896 unidades. Podemos prosseguir a divisão determinando
a parte decimal do quociente. Para a determinação dos décimos, colocamos uma
vírgula no quociente e acrescentamos um zero resto, uma vez que 896 unidades corresponde a
8.960 décimos.
Continuamos a divisão para determinar os
centésimos acrescentando outro zero ao novo resto,
uma vez que 960 décimos correspondem a 9600
centésimos.
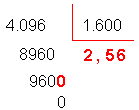 O quociente 2,56 é exato, pois
o resto é nulo. O quociente 2,56 é exato, pois
o resto é nulo.
Logo, o quociente de 4,096 por 1,6 é
2,56.
Operações com números
racionais decimais
| Igualamos as casas
decimais |
0,73 |
: |
5,00 |
| Suprimindo as
vírgulas |
73 |
: |
500 |
|
Efetuando a divisão
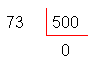 |
Podemos prosseguir a divisão, colocando uma
vírgula no quociente e acrescentamos um zero à
direita do três. Assim:
Continuamos a divisão,
obtemos:
|
Logo, o quociente de 0,73 por 5 é 0,146.
Em algumas divisões, o acréscimo de um zero
ao resto ainda não torna possível a divisão. Nesse caso, devemos colocar um zero
no quociente e acrescentar mais um zero ao resto. Exemplos:
|
|
Verifique 460 (décimos) é inferior ao
divisor (2.300). Colocamos, então, um zero no quociente e acrescentamos mais um
zero ao resto. |
Logo, o quociente de 2,346 por 2,3 é
1,02.
Observação:
Para se dividir um número decimal por 10, 100,
1.000, ..., basta deslocar a vírgula para a esquerda
uma, duas, três, ..., casas decimais. Exemplos:
Operações com números
racionais decimais
2º : Divisão não-exata
No caso de uma divisão não-exata
determinamos o quociente aproximado por falta ou por excesso.
Seja, por exemplo, a divisão de 66 por
21:
Tomando o quociente 3 (por falta), ou 4
(por excesso), estamos cometendo um erro que uma unidade, pois o quociente real
encontra-se entre 3 e 4.
Logo:
Assim, na divisão de 66 por 21, temos:
afirmar que:
3 é o quociente aproximado por
falta, a menos de uma unidade.
4 é o
quociente aproximado por excesso, a menos de uma
unidade.
Prosseguindo a divisão de 66 por 21,
temos:
Podemos afirmar que:
3,1 é o quociente aproximado
por falta, a menos de um décimo.
3,2 é
o quociente aproximado por excesso, a menos de um
décimo.
Dando mais um passo, nessa mesma
divisão, temos:
Podemos afirmar que:
3,14 é o quociente aproximado
por falta, a menos de um centésimo.
3,15 é o quociente aproximado por excesso, a menos de um
centésimo.
Observação:
-
As expressões têm o mesmo
significado:
- Aproximação por falta com
erro menor que 0,1 ou aproximação de décimos.
- Aproximação por
falta com erro menor que 0,01 ou aproximação de centésimos e, assim,
sucessivamente.
2. Determinar um quociente com
aproximação de décimos, centésimos ou milésimos significa interromper a divisão
ao atingir a primeira, segunda ou terceira casa decimal do quociente,
respectivamente. Exemplos:
13 : 7 = 1,8
(aproximação de décimos)
13 : 7 = 1,85 (aproximação de
centésimos)
13 : 7 = 1,857 (aproximação de
milésimo)
Cuidado!
No caso de ser pedido um quociente com
aproximação de uma divisão exata, devemos completar com zero(s), se preciso,
a(s) casa(s) do quociente necessária(s) para atingir tal aproximação.
Exemplo:
O quociente com aproximação de milésimos de 8 de 3,2
é
|
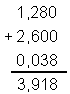
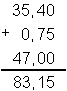
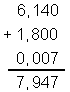
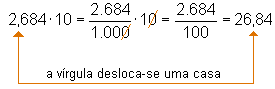
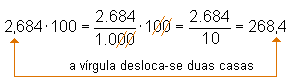
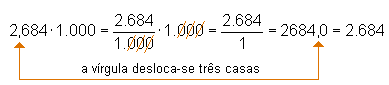
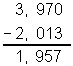
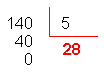
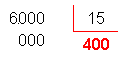
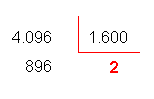
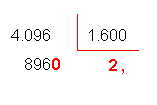
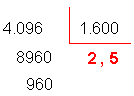
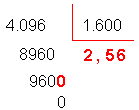 O quociente
O quociente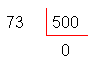
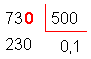
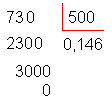
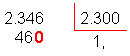
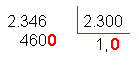
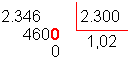
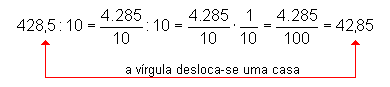
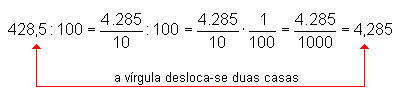
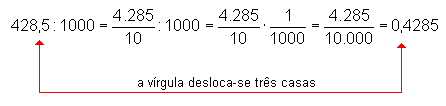



Nenhum comentário:
Postar um comentário